"Mahkum İkilemi" sayfasının sürümleri arasındaki fark
Ersin Kopuz (mesaj | katkılar) (" Mahkum ikilemi, sosyal bilimlerin popüler strateji oyunudur. İlk olarak 1950 yılında ortaya çıkmış bir kavramdır. John Von Neumann’ın "Oyun Teo..." içeriğiyle yeni sayfa oluşturdu) |
Ersin Kopuz (mesaj | katkılar) |
||
| 26. satır: | 26. satır: | ||
=Ayrıca Bakınız= | =Ayrıca Bakınız= | ||
| − | '''Film:''' The Dark Knight | + | '''İlgili Film:''' The Dark Knight |
| − | '''Kitap:''' Stuart Sutherland’in- İrrasyonel | + | '''İlgili Kitap:''' Stuart Sutherland’in- İrrasyonel |
16.57, 9 Temmuz 2021 tarihindeki hâli
Mahkum ikilemi, sosyal bilimlerin popüler strateji oyunudur. İlk olarak 1950 yılında ortaya çıkmış bir kavramdır. John Von Neumann’ın "Oyun Teorisi"ni ilk kez kullanmıştır. John Forbes Nash teoriyi geliştirerek ünlenmiştir. Oyun teorisi temelde yaşam oyununda başarılı olma stratejilerini geliştirmekle ilgilidir. En rasyonel faydayı getirebilecek çözümün bulunmasında kullanılan bir yöntemdir. Kavramın temelinde Nash Dengesi yatmaktadır. [1] Teori de tarafların stratejilerinin mantığını anlama ve matematiksel hesaplamalarla en uygun stratejiyi bulma amacına hizmet eder. Teori de geçen oyun kavramı gerçek anlamı yansıtmamaktadır. Burada iyi tanımlanmış bir çatışma durumunu anlatmak için “oyun” kavramı kullanılmaktadır. Oyun, iki veya daha fazla oyuncunun tercih edebileceği alternatifler arasından seçim yaptığı bir durumdur. Seçim sonuçları oyunun da sonucunu belirlemektedir. Sonuçlar için tercihlerin sırasının oyuncular için farklı olduğu varsayılır. Bu nedenle oyuncuların ilgileri çoğunlukla çatışma halindedir. Mahkum ikilemi paradigmatik, bireysel ve işbirliğine dayalı bir oyundur. [2]
Senaryo
Polis iki zanlı adam tutuklar. Fakat polisin elinde onları tutuklamak için yeterli kanıt bulunmamaktadır. Bu nedenle farklı mahkum bölmelerinde bulunan her iki adam ayrı ayrı ziyaret edilerek kendilerine değişik teklifler sunarlar. [3] Başlarda sessiz kalmak iyi bir strateji olarak gözükebilir. Fakat zanlılar birbirlerinin düşüncelerini bilmediklerinden ve işbirliği yapamadıklarından dolayı bireysel çıkarlara göre hareket etme eğilimdedirler. Bu durum ise oyunun sonucunda belirleyici bir faktör olacaktır. [4]
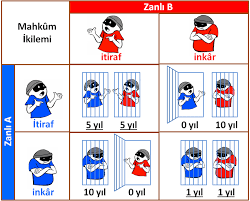
Teklifler şu şekildedir; eğer zanlılardan biri suçunu itiraf ettiği takdirde diğeri inkar ederse, itiraf eden serbest kalacak inkar eden zanlı ise 10 yıl hapse mahkum edilecektir. Eğer her iki zanlı da suçunu inkar ederse, her iki zanlı da 1 yıl hapse mahkum edilecektir. Eğer her iki zanlı da suçunu itiraf ederse, her ikisi 5'er yıl hapis cezasına mahkum olacaklar. Bu durumda her iki zanlı itiraf etmek veya inkar etmek arasında tercih yapmak zorunda bırakılmaktadır. Her iki zanlıya da soruşturma sonuna kadar birbirleri ile iletişim kurma imkanı vermediklerinden dolayı diğerinin kararını öğrenme imkanı yoktur. Baskın strateji 5,5'dir ve her ikisi için en karlı yol 1,1'dir. Tutsak ikilemindeki gibi bazen iki oyuncu için de kötü olan sonuçların ortaya çıkmasına neden olabilecek Nash dengesi ortaya çıkmaktadır. [5]
Çıkarım
- Mahkumlar ikilemi kuramı en çok liberalizmin ilgi alanına girmektedir. Bunun nedeni zanlıların uzun vadede çıkarı için işbirliğine girmesimin gerekli olmasıdır.
- Neo-realist bakış açısı ise oyuna, devletler birbirlerinin güvenliğinde tehdit oluşturabilecekleri bir işbirliği gerçekleşmeyeceği düşüncesiyle yaklaşmaktadırlar.
- Kurumsalcılar, mahkum açmazının kurumlarla ve iletişimle üstesinden gelinebileceğini savunurlar.
- Olgusalcılar devletin kimlik paylaştığını belirterek kuramın kimliklerini, kuramın normları ihmal edeceğini savunarak yararsız bulmaktadırlar.
Gerçek dünyadaki durumlarda dayanışma probleminin ilk örneği olmasından dolayı uygulanabilmektedir.
Teori; politika, sosyoloji, biyoloji, etnoloji ayrıca silahlanma yarışı ve diğer sosyal bilimlerde uygulanabilmektedir. Teoriden farklı olarak uygulandığında kişilik yapısı etkili olacağından oyunda farklı sonuçlar ortaya çıkabilmektedir. Bu durumda mahkum ikilemi oyunu, Nash dengesi ile çelişmektedir. Nash, her oyuncunun kendi en iyi stratejisini izleyeceğini, bunun nedeni olarak ise diğer oyuncuların da aynısını yapacağını var saymaktadır. Fakat oyun bize bunun her durumda geçerli olmayacağını göstermektedir. Nash bu tür oyunlardaki kısır döngüyü çözmek için bir öneri ortaya atmaktadır. Ona göre, kişilerin kendine en yüksek faydayı sağlayacak stratejisi bulunmaktadır. Ancak “dominant strateji” olarak nitelendirilen bu stratejide oyun tek kişilik olmadığından strateji uygulanamamaktadır. Kişiler bir denge durumuna mecbur kalmaktadırlar. Nash matematiği kullanarak böyle bir dengenin her koşulda mevcut olacağını kanıtlamakta ve oyun teorisinin birçok alanda kullanılmasını sağlamaktadır. [6][7]
Ayrıca Bakınız
İlgili Film: The Dark Knight
İlgili Kitap: Stuart Sutherland’in- İrrasyonel
Hazırlayan: İrem Topuk
- ↑ Özdil A. (2016)- Evrim Ağacı- Tutuklu İkilemi Üzerinden Nash Dengesi'ne Kısa Bir Bakış
- ↑ Şener E.- Toktaş İ, (2015) Akademik Platform, Kritik Düşünme Ekseninde Empati ve Mahkûm İkilemi
- ↑ Şener E.- Toktaş İ, (2015) Akademik Platform, Kritik Düşünme Ekseninde Empati ve Mahkûm İkilemi
- ↑ Özdil A. (2016)- Evrim Ağacı- Tutuklu İkilemi Üzerinden Nash Dengesi'ne Kısa Bir Bakış
- ↑ Şener E.- Toktaş İ.(2015) Akademik Platform, Kritik Düşünme Ekseninde Empati ve Mahkûm İkilemi
- ↑ Erdoğmuş N.(1995) İstanbul Üniversitesi Sosyal Bilimler Enstitüsü İşletme Fakültesi, Rekabet-İşbirliği İkilemi ve Politik Davranışa Dönüşme Süreci
- ↑ Urgancı B. (2014) Tuiç Akademi- Tutsak İkilemi